A három szempont

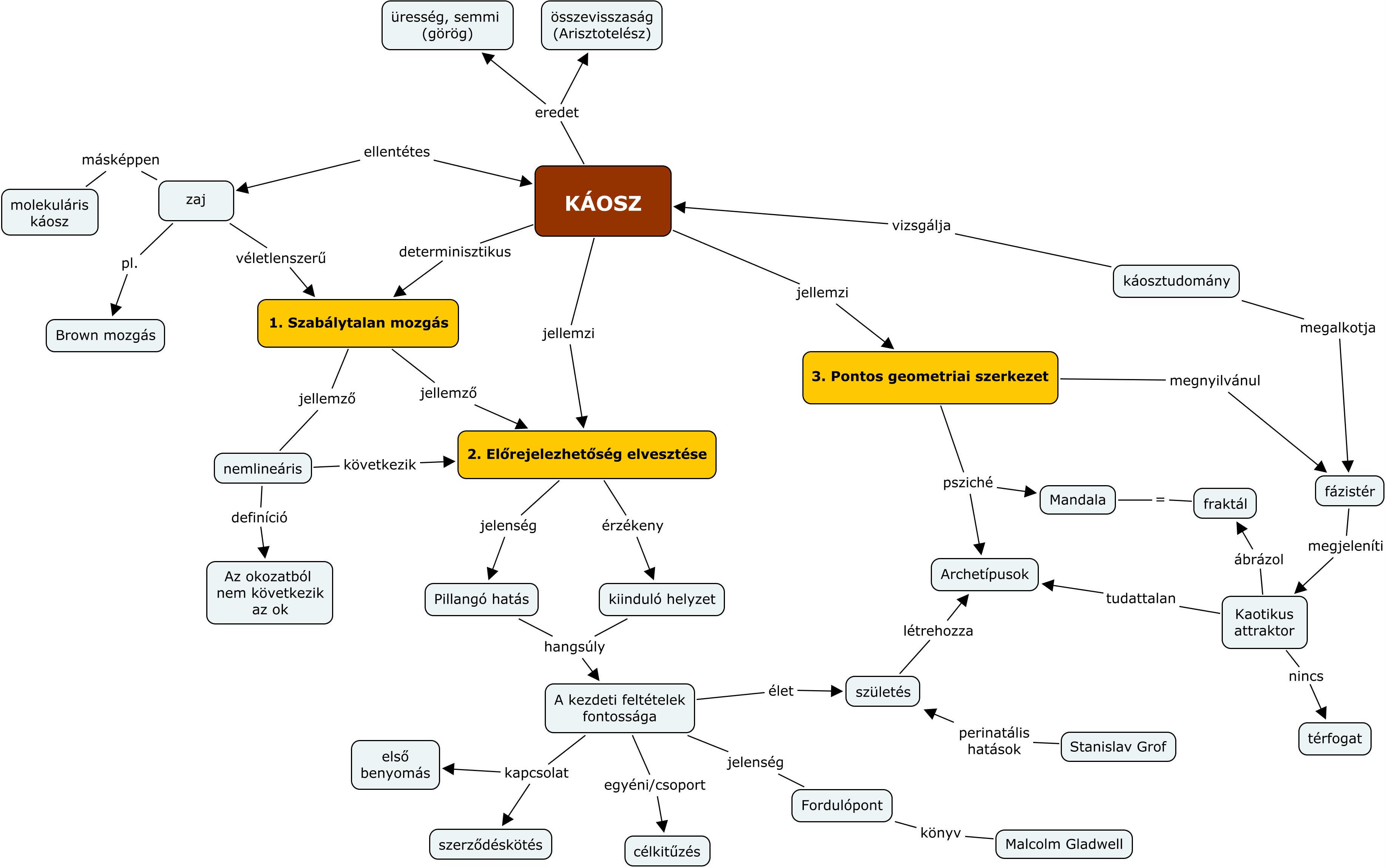
A káoszelmélet pontosan az ilyen problémák megoldására jött létre. A fizikában zajként jelölik a teljességgel megjósolhatatlan, véletlenszerű jelenségeket. A káoszt ehhez képest jellemzi egyfajta determinizmus, jóllehet a zajhoz hasonlatosan véletlenszerűnek tűnő szabálytalan mozgást ír le. Tél Tamás cikke nyomán három oldalról lehet a káoszt összefoglalni:

1. Szabálytalan mozgás
2. Előrejelezhetőség elvesztése
3. Pontos geometriai szerkezet

Pillangó hatás

"Kis különbségek a kezdeti feltételekben nagyon nagy különbségeket okoznak a végső jelenségben." A pillangó-hatás elv arra a törvényszerűségre utal, hogy egy káosz jellegű jelenség lefolyását a kezdeti állapot nagy mértékben befolyásolja. Csak egy kicsit változtass a kezdeti feltételeken, és ezáltal a későbbi állapot merőben különbözni fog! A pillangó-hatást a Butterfly effect c. film jól illusztrálja abban a formában, ahogy az a köztudatban (tévesen) elterjedt.

Érdemes elolvasni Mérő László rövid esszéjét az ismeretlen ismeretterjesztő káoszelméleti mellélövéséről:

Az ismeretlen ismeretterjesztő talált egy szép hasonlatot, és az egész világon divatba jött a káoszelmélet. Meglebbenti egy pillangó a szárnyát Tokióban, és ettől hatalmas vihar kerekedik New Yorkban - mondta az ismeretlen ismeretterjesztő, és ettől mindenki úgy érezte, hogy most már érti a káoszelméletet, világos, mi az a pillangóeffektus. Pedig Tokióban, akárcsak a hűvösvölgyi Nagyréten, a lepkék állandóan verdesnek a szárnyaikkal, és szerencsére ehhez képest ritkák New Yorkban a viharok. A tornádót akkor sem egy tokiói lepke okozza, ha nélküle hét ágra sütne a nap New Yorkban. [...] Mire használható akkor a káoszelmélet? Arra semmi esetre sem, amire a leggyakrabban használják: ijesztgetésre.[...] Márpedig a legújabb kutatásokban sok jel mutat arra, hogy a tudattalan működése is többé-kevésbé megfelelhet a káoszelmélet modelljeinek. Könnyen lehet, hogy a káoszelmélet egy olyan mechanizmust ír le, amely a természet egyik alapvető működési elve, bár egyelőre még nem ismerjük ennek az elvnek az érvényességi körét. (Mérő László: Maga itt a tánctanár?)

Ajánlott irodalom

1. Tél Tamás: A káosz természetrajza Jó bevezetés a káoszelméletbe. A fenti fogalomtérképet ezen cikk alapján készítettem.
2. Mérő László: Maga itt a tánctanár?
3. Malcolm Gladwell: Fordulópont
4. Renata Phelps: Developing online from simplicity toward Complexity: Going with the Flow of Non-Linear Learning Ez az egyedüli cikk, melyet ajánlani tudok a cck08 ezen hétre szóló irodalomjegyzékből. Az összes többit érdektelennek találtam, ami persze lehet, hogy csak engem minősít... A jelen tanulmányban emlegetett kurzus deklarált célja az volt, hogy arra bíztassa a jövő pedagógusait, hogy megértsék és alkalmazzák az internet adta tanulási stratégiákat, attitűdöket és készségeket. A Web egy hatalmas pók által szőtt hálóhoz hasonlatos. Nincs benne kiindulási és befejezési pont. Annyira sok információ van jelen az Interneten, hogy nem lehet célunk mindet feldolgozni: a legnagyobb igyekezettel is csak egy kis részletével találkozhatunk csupán. A Web roppant hatékony tanulmányi közeg. Majdnem bármilyen szakmai kihívásnak próbálunk eleget tenni, a világhálón fellelhető információk ma már nélkülözhetetlen támpontot jelentenek. Egy ilyen környezetben való tanulás eleinte zavaró lehet, hiszen hozzászoktunk ahhoz, hogy a tanár pontosan megmondja azt, hogy honnan hová kell tartanunk. Fel kell ismernünk, hogy a világról alkotott tudásunk redukálhatatlanul összetett; nem az a feladat, hogy egyes emlékeket elemezzünk, hanem az, hogy egységében képesek legyünk érteni és használni ezt a komplexitást. így juthatunk el a legmagasabb formájú megismeréshez: az intuícióhoz. A tudáshálónk nagy része implicit, azaz direkt módon nem hozzáférhető a tudat számára. Az intuíció az egyedüli kognitív apparátus, mely ebből a rendszerből átfogó, integratív megismerési élményt hoz létre. Minél inkább a figyelünk a tudás hálózati jellegére, annál inkább a szemantikai mélységet vizsgáljuk. A fogalmak/kijelentések közötti kapcsolatok jellege határozza meg azt, hogy milyen mélységű tudással rendelkezünk az adott területen. A redukcionista gondolkodásmódnak feltétlenül ki kell egészülnie egy integratív szemlélettel, mely a témák közötti átjárhatóságot biztosítja. Ezért helytelen a Polgár-féle zseninevelés redukcionizmusa: szükség van a sokszínűségre, ha a tudás gyarapítása a cél. Az önvezérelt tanuláshoz elengedhetetlenül szükséges megtanulnunk célokat kitűzni. A helyes célkitűzéshez ismernünk kell a területet, az azonban nem mindig adott. Nem mindig vagyunk tisztában azzal, hogy mit nem tudunk! Ahhoz, hogy körvonalazódjon a terület, melyről tudásunkat bővíteni kívánjuk, fel kell fedeznünk azt, játékra és nyitottságra van szükségünk. Ez nem egy célirányos, konvergens tanulási folyamat, hanem teljes mértékben kaotikus, divergens. A cikkben bemutatott kutatás során kifejlesztett non-lineáris tanulmányi közeg célja pontosan ez a fajta kaotikus, felfedező, játékos tanulás szorgalmazása volt.

Kérdések

1. Mi a káosz három jellemzője?
2. Miért meghatározó élmény a születés (káoszelméleti szemszögből)?
3. Mit hívunk kaotikus attraktornak?
4. Miben hiányos (téves) a köztudatban elterjedt pillangó-hatás elv?
5. Mi a különbség a zaj és a káosz között?
6. Milyen összefüggés van a tanulás és a káosz között?
7. Mit gondolsz, a krízishelyzetek hogyan függnek össze a káosszal?

Végezetül következzen egy rövid előadás arról, hogy az alulról felfelé szerveződő közösségek miként kezdik ki a szociális hierarchiákat.